1. 모델평가
1.1 모델 평가란?
- 생성한 모델을 좋다, 나쁘다, 그저 그렇다 라고 평가할 방법은 사실 없다
- 대부분 다양한 모델, 다양한 파라미터를 두고, 상대적으로 평가를 한다
2. 회귀 모델
2.1 회귀모델의 평가
- 회귀 모델은 실제 값과의 에러치를 가지고 평가를 함
2.1.1 MAE (Mean Absolute Error)
- y에서 예측값을 뺀 수치에 절대값(Absolute)을 취하고 모두 더한뒤 N으로 나눠준것
- MSE보다 특이치가 덜 민감하다.
- 다만 절대값을 취하기 때문에 모델이 Underperformance인지, Overperformance인지 모른다
- Underperformance : 모델이 실제 값보다 낮은 값으로 예측함
- Overperformance : 모델이 실제 값보다 높은 값으로 예측함
2.1.2 MSE (Mean Squared Error)
- y에서 예측값을 뺀 수치에 제곱(Squared)을 하고 모두 더한뒤 N으로 나눠준것
- 제곱을 하기에 모델의 예측값과 실제값 차이의 면적의 합이다
- 만일 특이값이 존재한다면, 수치가 높아진다(특이값에 민감하다)
2.1.3 RMSE (Root Mean Squared Errir)
- MSE에 루트를 씌어준 것
- 제곱에 다시 루트를 씌워준것으로 실제 값과 비슷한 단위로 변환되어 해석이 된다.
2.1.4 R2 Score (Coefficient of Determination, 결정계수)
- RMSE, MAE는 데이터 마다 값이 다르기 때문에 값만 보고 바로 성능을 판단하기 어렵다.
- 하지만 R2 Score는 상대적인 성능이므로, 직관적으로 알기 쉽다. (1에 가까우면 좋은 성능)
- 추정한 선형 모형이 주어진 자료에 얼마나 적합한지를 재는 척도이다. 즉, 반응 변수의 변동량 중에서 적용한 모형으로 설명가능한 부분의 비율을 가리킨다.
- -1 ≤ r ≤ 1
- 0 ≤ R2 = SSR/SST ≤ 1
- 총 제곱합(total sum of square)이 SST, 회귀 제곱합(regression sum of square)이 SSR, 잔차 제곱합(residual sum of square)이 SSE이다
3. 이진 분류모델
3.1 Confusion Matrix
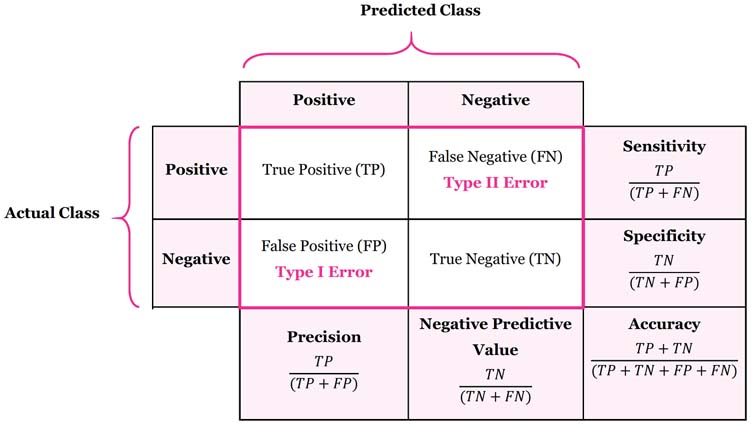
- TP (True Positive) : 실제 Positive를 Positive로 예측한것
- FN (False Negative) : 실제 Positive를 Negative로 예측한것 (1종 오류)
- TN (True Negative) : 실제 Negative를 Negative로 예측한것
- FP (False Negative) : 실제 Negative를 Positive로 예측한것 (2종 오류)
3.2 Accuracy, Precision, Recall, Fall-Out
- Accuracy(정확도) : 전체 데이터 중 맞게 예측한것 TP + TN / TP + FN + TN + FN
- Precision(정밀도) : 양성이라고 예측한것 중 실제 양성의 비율 TP / TP + FP (True라고 예측한것 중에 실제 True)
- Recall(재현율) : 참인 데이터 중에서 참이라고 예측한것 TP / TP + FN (True 데이터 중에서 True라고 예측한 것)
- Fall-out(위양성율) : 실제 양성이 아닌데 양성이라고 잘못 예측한것 FP / FP + TN (False 데이터 중에서 양성이라고 잘못 예측한것)
3.2.1 Recall, Precision 정리
- Recall : 참인 데이터 중에서 참이라고 예측한 데이터의 비율
- Precision : 참이라고 예측한것 중에서 실제 참인 데이터
- threshold : 양성으로 판단하는 기준
- 그러나 Recall과 Precision은 서로 영향을 주기 때문에 한 쪽을 극단적으로 높게 설정해서는 안됨
3.2.2 Recall, Precision의 예시
- 재현율(Recall) 예시 : 실제 양성인 데이터를 음성이라고 판단하면 안되는 경우라면, 재현율(Recall)이 중요하고 이 경우는 Threshold를 0.3 혹은 0.4로 선정
- 실제 양성(1 = 암환자)를 음성(0 = 정상인)이라고 판단하면 안되는 경우라면 재현율(Recall)이 중요하고 0(음성)과 1(양성)을 결정하는 Threshold를 낮춰서 1의 확률을 높임(ex : 0.3 이상이면 1) (eg. 암환자 판별)
- 암환자를 암환자가 아니라고 판단하면 문제가 커짐
- 정밀도(Precision)실제 음성인 데이터를 양성이라고 판단하면 안되는 경우라면, 정밀도(Precision)이 중요하고, 이경우는 Threshold를 0.8 혹은 0.9로 선정
- 실제 음성(0 = 정상메일)인 데이터를 양성(1 = 스팸매일)이라고 판단하면 안되는 경우라면 정밀도(Precision)가 중요하고 이경우는 Threshold를 높여 1이 잘 안나오게 한다. (eg. 스팸 메일)
- 중요한 메일을 스팸메일로 판단하면 문제가 커짐
3.3 F1 Score
- F1 = (1 +1(B) * (precision * recall) / (1(B) * precision +recall)
- 여기서 B가 1이 아니면 FB 스코어라고 한다.
- F1-score는 Recall과 Precision을 결합한 지표
- Recall과 Precision이 어느한쪽으로 치우치지 않고 둘다 높은 값을 가질수록 높은 값을 가짐
3.4 ROC 곡선

- FPR (False Positive Rate)이 변할 때, TPR(True Positive Rate)의 변화를 그린 그림
- FPR을 x축, TPR을 y축으로 놓고 그림
- TPR은 Recall을 의미, FPR은 Fall-out을 의미
- 직선에 가까울수록 머신러닝 모델의 성능이 떨어지는것으로 판단
3.5 AUC
- ROC 곡선 아래의 면적
- 일반적으로 1에 가까울수록 좋은 수치
- 기울기가 1인 직선 아래의 면적이 0.5 -> AUC는 0.5보다 커야함
4. 실습) ROC 커브 그리기
4.1 데이터 불러오기
1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
red_wine = pd.read_csv(red_url, sep = ';')
white_wine = pd.read_csv(white_url, sep = ';')
red_wine['color'] = 1
white_wine['color'] = 0
wine = pd.concat([red_wine, white_wine])
wine['taste'] = [1. if grade > 5 else 0. for grade in wine['quality']]
X = wine.drop(['taste', 'quality'], axis = 1)
y = wine['taste']
4.2 간단히 결정나무 적용해보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=13)
wine_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
wine_tree.fit(X_train, y_train)
y_pred_tr = wine_tree.predict(X_train)
y_pred_test = wine_tree.predict(X_test)
print('Train Acc : ', accuracy_score(y_train, y_pred_tr))
print('Train Acc : ', accuracy_score(y_test, y_pred_test))
1
2
Train Acc : 0.7294593034442948
Train Acc : 0.7161538461538461 <br>
4.3 각 수치 구해보기
1
2
3
4
5
6
7
8
from sklearn.metrics import (
accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve)
print('Accuracy : ', accuracy_score(y_test, y_pred_test))
print('recall_score : ', recall_score(y_test, y_pred_test))
print('precision_score : ', precision_score(y_test, y_pred_test))
print('roc_auc_score : ', roc_auc_score(y_test, y_pred_test))
print('f1_score : ', f1_score(y_test, y_pred_test))
1
2
3
4
5
Accuracy : 0.7161538461538461
recall_score : 0.7314702308626975
precision_score : 0.8026666666666666
roc_auc_score : 0.7105988470875331
f1_score : 0.7654164017800381 <br>
4.4 ROC커브 그리기
1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
pred_proba = wine_tree.predict_proba(X_test)[:, 1]
fpr, tpr, thresholds = roc_curve(y_test, pred_proba)
plt.figure(figsize=(10, 8))
plt.plot([0,1], [0,1])
plt.plot(fpr, tpr)
plt.grid()
plt.show()
